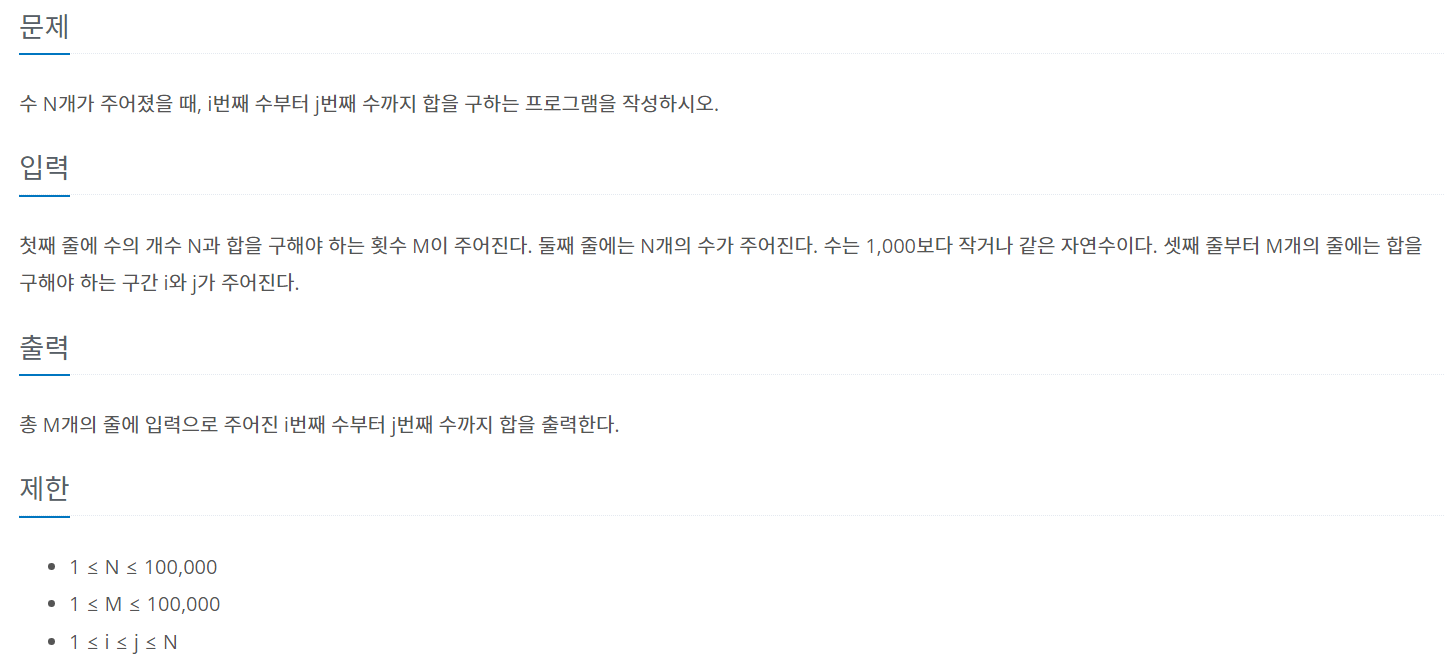
구간합 개념을 제대로 잡을 수 있는 문제였다.
i부터 j 까지의 누적합을 구할 때는 처음부터 배열에 더한 값을 저장해놓으면 금방 구할 수 있다.
코드에 주석을 자세하게 달아놓았다.
package Beakjoon;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class Main_11659 {
/*
N개의 수가 주어졌을 때 i~j 까지의 합을 구하기
누적합 문제 -> 앞에서부터 애초에 더한 다음 배열에 저장하자
*/
static int N; //수의 개수
static int M; //합을 구해야 하는 횟구
static int [] arr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
//전역변수 초기화
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr = new int [N+1]; //인덱스 맞춰주기 위함
//배열 채우기
st = new StringTokenizer(br.readLine());
for(int i=1; i<=N; i++){
arr[0] = 0;
//앞에서부터 차례대로 더한 값을 배열에 저장
arr[i] = arr[i-1] + Integer.parseInt(st.nextToken());
}
//M만큼 반복돌기
for(int i=0; i<M; i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
//구하고자 하는 범위의 끝 값에서
//구하고자 하는 범위의 시작값 -1 을 해주면 쉽게 구할 수 있다
sb.append(arr[end]-arr[start-1]).append("\n");
}
System.out.println(sb);
}
}'알고리즘 > BeakJoon' 카테고리의 다른 글
| 백준 2798 블랙잭 Java (0) | 2023.02.28 |
|---|---|
| 백준 2210 숫자판 점프 Java (0) | 2023.02.28 |
| 백준 2003 수들의 합 2 Java (0) | 2023.02.23 |
| 백준 1941 소문난 칠공주 Java (0) | 2023.02.23 |
| 백준 14503 로봇청소기 Java (0) | 2023.02.20 |
